Regression in Machine Learning - Linear and Non-Linear Regression

Hello Readers!! Hope you are doing well. As told in previous article, today we will start with regression-based machine learning techniques. Regression analysis is based on the relation of input and output, i.e., for a given input, we need to predict the output. For a model with good accuracy, all the data points must follow a pattern and any data point must not have large spatial distance from other points. 

Today we will discuss linear and non-linear regression-based machine learning techniques. 

Linear Regression

Just so you know, this definition is going to be the most difficult definition of your academic life. Linear regression means output functions have linear relationships with input functions (It was a joke obviously 😅). But, on a serious note, a linear regression network is commonly used to train a new dataset. Linear relation is given by:

where ‘y’ is output data, ‘x’ is the input data, ‘a’ and ‘b’ are constants. Key points are as follows:

• Used for easy predictions and fast fitting models.
• It is considered as a reference algorithm for other complex regression-based machine learning techniques.

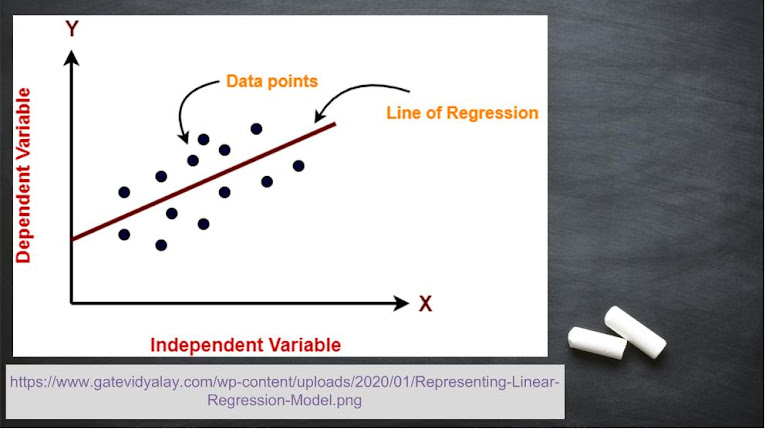
Non-Linear Regression

It is used when there is non-linear relationship between output and input variables, irrespective of the fitness of the model. Non-linear equation is given by:

where ‘n’ can be any number but 0 or 1. Key points are as follows:

• It is only used when there is no alternative to improve the fitness of the function.
• It is based on parametric assumptions.

Now the question arises, “What are parametric assumptions?”

When the dataset used to train a network belongs to only one domain, say animals, we can have pictures of dogs, cats, and tigers, but we cannot have pictures of roses, sunflowers, or other flowers, then the model is said to have parametric statistics.

Gaussian Process

If images from animals, flowers and other domains are used for training, the model is said to have non-parametric statistics. When the decision is uncertain, spatial analysis (i.e., qualitative and quantitative analysis of computed images) is performed. The trained model is called gaussian process regression model. This property of training the model using datasets of more than one domain is called interpolation. And the estimation of uncertainty using the interpolation is called Kriging. The interpolated values are termed as Best Linear Unbiased Predictors (BLUP). Some applications of gaussian process regression model are as follows:

• To optimize the complex models such as automotive engines.
• Ground water distribution by performing interpolation on hydrogeological data.

Reference: Machine Learning with MATLAB (eBook)

We will continue with more regression-based machine learning techniques in our next article. Please give your feedback on this article of Deep Learning Series and suggestions for future articles in the comment section below 👇.